《怎样解题》 陈章鱼解读

《怎样解题》| 陈章鱼解读

关于作者

乔治·波利亚。他曾经担任瑞士苏黎世工业大学的数学系主任。后来，波利亚移居美国，担任布朗大学和斯坦福大学的教授，并且当选美国国家科学院院士，成为世界知名的数学家。

关于本书

波利亚一直致力于研究数学思维的一般规律。在这方面，他出版过多部名著，最著名的就是这本《怎样解题》。这本书出版已经将近80年，依然畅销不衰。在这本书中波利亚讲解的不是具体的数学知识，而是解答数学问题的底层逻辑。

核心内容

本书围绕“探索法”这一主题，采用明晰动人的散文笔法，阐述了求得一个证明或解出一个未知数的数学方法。并且将这样的方法，迁移到更广阔的场景中。

就像波利亚在书中所说：「解题是一种实践性技能，我们可以通过模仿和实践来学会任何一种实践性技能。」我们平时所说的洞察力、判断力、创造力、思维能力等，其实可以通过不断模仿和实践解题技巧来提高。

你好，欢迎每天听本书，我是陈章鱼。今天为你解读的这本书叫《怎样解题》，副标题叫《数学思维的新方法》。

这本书的作者，是一位名副其实的数学大神，乔治·波利亚。他曾经担任瑞士苏黎世工业大学的数学系主任，这个苏黎世工业大学，就是爱因斯坦的母校。后来，波利亚移居美国，担任布朗大学和斯坦福大学的教授，并且当选美国国家科学院院士，成为世界知名的数学家。

波利亚不仅是一位杰出的数学家，也是一位数学教育家，一直致力于研究数学思维的一般规律。在这方面，他出版过多部名著，最著名的就是这本《怎样解题》。这本书出版已经将近80年，依然畅销不衰。

这本书之所以受到大家的追捧，是因为波利亚讲解的不是具体的数学知识，而是解答数学问题的底层逻辑。因此，这本书成为无数学习数学的朋友刻苦钻研的武林秘籍。

有一位享誉世界的华裔天才数学家陶哲轩，31岁就获得数学界的诺贝尔奖——菲尔兹奖，32岁当选英国皇家学会会士。他还有一项至今无人打破的记录，就是12岁获得了国际数学奥林匹克竞赛的金牌，他就极为推崇波利亚的数学思维，用这样的方法准备国际数学奥林匹克竞赛。后来，他写了一本书叫《陶哲轩教你学数学》，其中的第一章《解题的策略》，完全介绍的是波利亚在《怎样解题》中的策略。

你可能会问，那我们大多数人，现在既不搞数学研究，也不参加数学竞赛，花 20 多分钟听一本书，给我们讲的都是怎么解数学题，这有什么意义呢？

当然有意义。因为波利亚的数学思维，不止可以用在代数、几何这样的数学问题上，还可以迁移到更广阔的场景中。

我们每天都需要解决各种生活中的问题，小到衣食住行，大到人生抉择，波利亚在《怎样解题》中提供的思考方法，都能帮助我们更好地解决这些问题。

更关键的是，解决问题是一种技能，可以通过不断地实践来提升。就像波利亚在书中所说：「解题是一种实践性技能，我们可以通过模仿和实践来学会任何一种实践性技能。」我们平时所说的洞察力、判断力、创造力、思维能力等，其实可以通过不断模仿和实践解题技巧来提高。

所以，在为你解读这本书时，我会尽量减少对具体数学问题的解析，把更多的注意力放在波利亚对思维的点拨上。因为这些经验和智慧，我们可以灵活运用在日常的工作和生活中。

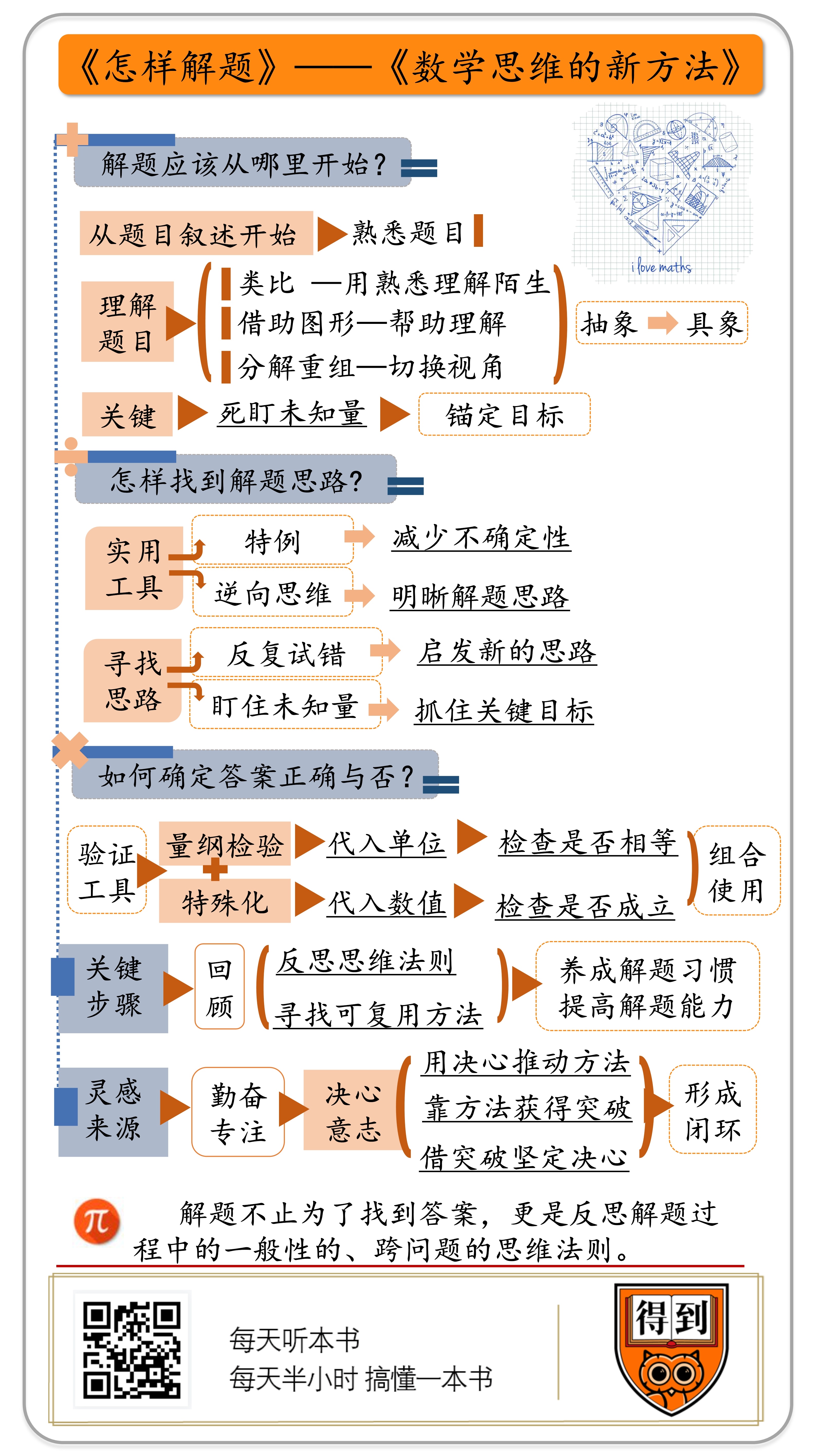
所谓万事开头难，解题也是一样。当我们面对一道问题，我们应该从哪里开始呢？

波利亚告诉我们，应该从题目的叙述开始，让自己熟悉题目并且理解题目。

请注意，这个过程听起来挺平常的，实际上至关重要。因为理解题目的过程，就是你制定目标的过程。你的目标越清晰，你越知道自己接下来应该用什么样的策略对待这道题目，同时，你也能把更多的注意力放到解题的过程中。

你可能会说，我知道理解题目很重要，但是你光这么说，看不懂的题我还是看不懂啊。别着急，波利亚在这本书中，就介绍了几种非常好用的方法，帮助我们更快速地理解题目。

第一种方法，叫做类比。核心的策略是，找一种我们熟悉的东西，它的特性和题目类似，这样，我们就能借助熟悉的东西去理解陌生的东西。

比如，爱因斯坦对时间的描述，这就是一个类比。他认为时间就像一个空间上的坐标轴，有长短，有方向，有刻度。但是，这是时间的真实状态吗？未必。但是，只有通过这种类比的方式，我们才能用空间，这个熟悉的东西，去理解时间这个陌生 的东西。

这就是类比的最大好处，能将陌生的问题转化为熟悉的问题。而这恰恰是数学家们最擅长的。

有一个笑话：一位数学家想改行，去消防队应征消防员，消防队长说那我面试一下你，带数学家去了消防队后边的小巷，巷子里有一间仓库，一个消防栓和一卷软管。

消防队长问：「如果仓库起火了，你怎么办呢？」数学家说：「我把软管接在消防栓上，打开水龙头，把火浇灭。」

消防队长说：「不错不错。那如果仓库没有起火，你怎么办呢？」数学家想了半天，说：「那我就把仓库点着。」消防队长说：「啊？为什么啊？」

数学家说：「这样，我就把问题简化为一个我已经解决过的问题了。」

这个段子是吐槽数学家的，实际情况当然不会这样，但是我们能看出一点，那就是用已经解决过的问题，去类比尚未解决的问题，这是数学家们经常使用的思维方式。

第二种方法是借助图形。如果你翻一下波利亚的著作，你会发现他有一个习惯，他在分析题目时，能不用公式就不用公式，可是只要能用图形，他就一定会画图。

如果面对的是几何问题，我们当然要画图，可是面对其他问题，波利亚也强烈建议我们用图形帮助我们理解题目。

第三种方法叫做分解和重组。

这个方法的核心策略，是像电影镜头一样，在整体和细节之间切换观察。

为什么要切换观察呢？因为如果你深入到细节中去，就有可能在细节中迷失自我。它们会阻碍你对要点投入足够的注意力，甚至会使你全然看不到要点。

但困难在于，我们事先不可能知道哪些细节最终会是必要的，那些又不会是。如果全不看细节，只考虑整体，又未必能深入理解题目。

所以，聪明的做法是，切换视角。先整体观察题目，然后观察细节，一个细节打动了你，于是你对它集中注意力，接下来再观察另一个细节，每个细节都观察到之后，再回到整体。

最后是把不同的细节组合起来，看看能不能有新的收获。

这么介绍三种方法，可能会显得有些空泛，别着急，一会儿我会用一道具体的题目举例，看看这些方法怎样应用。

咱们先总结一下三个方法的共性，回过头来看，三种方法的背后，其实是一个基本策略，那就是尽可能清晰、生动地使整个题目形象化。如果能把抽象的概念变得形象化，就说明你已经成功地理解题目了。

除此之外，波利亚还特别提醒我们，在理解问题的时候，你要死死盯住一点，什么呢？就是题目中的未知量。

咱们用一道具体的问题举例，来看看这些方法怎么使用。你放心，这道题中既没有烧脑的定理，也没有复杂的数字，这道题是这样的：一只熊向正南走一公里，然后改变方向，向正东走一公里，然后再向正北走一公里，此时它正好回到了起点，请问，这只熊是什么颜色的？

这道题听起来不复杂，不过答案也不太容易想出来。咱们一起来分析一下，这道题的未知量是什么？是一只熊的颜色。但是怎么能从数学数据中得出一只熊的颜色呢？这就有点奇怪。

那咱们再看已知量，进入到细节中，你可以在纸上画一张图，就会发现，正常情况下，向南一公里，向东一公里，再向北一公里，应该再向西走一公里，才能回答出发点，为什么这只熊按照题目描述的方式，只走了三公里，就回到出发点呢？

这个矛盾点，才是这道题真正的未知量。

那咱们把这些细节组合一下，走三条线，回到起点，那就应该是个三角形。

向南、向东、再向北，可以走出一个三角形吗？

有了。站在北极点，朝着任何一个方向走，都是向南走，而从任何一个位置向着北极点走，都是向北走。这样，这只熊从北极点出发，向南、向东、向北，就可以走一个三角形，回到出发点。

既然是北极点附近，那么这只熊应该是一只北极熊，当然就是白色的。

你看，抓住未知量，你就抓住了问题的关键。类比、画图，还有分解和重组，这些方法能帮助你更好地理解题目。

完成了前边的步骤，我们就充分地理解了题目，知道我们的目标是什么了。接下来遇到的问题就是，怎样找到解题思路？

这个问题可能是你最关心的，因为所谓的「思路」这个东西，实在是太玄妙了。它看不见摸不着，以至于我们大多数时候，都觉得要靠灵感，就像动画片里一样，脑中一个小灯泡突然亮起来，就算有了思路。

其实，寻找思路用不着干等。在这一步，波利亚也给我们提供了两种非常好用的工具。

第一个工具，叫做「特例」。当没有思路的时候，不妨用特例帮助自己思考。

一个泛泛的问题，往往让人有一种无法把握、无从下手，无法抓住里边的任何东西的感觉，这是因为条件太多，所以看起来从哪个条件都没法入手。正所谓乱花渐欲迷人眼，一个泛泛的问题，往往有一种不确定性。这种不确定性，就会成为思维的障碍。

那怎么减少这种不确定性呢？可以先考虑一个特例，这样就能使得问题的条件确定下来，帮助我们探一探问题的内部结构。

第二个工具，叫做「逆向思维」。正面思考感觉茫然的时候，不妨尝试反过来推导。

很多人推崇逆向思维的力量，比如查理·芒格在《穷查理宝典》当中有一句名言：「反过来想，永远要反过来想。」

举个例子，咱们来看这么一道题，你站在河边，身边有两个桶，大桶能盛9升的水，小桶能盛4升的水，我的问题是，你要怎么样做，才能盛出6升的水来呢？

这道题用逆向思维来思考，从结果向前推，你会发现更容易得出答案。

6升的水，肯定放不进4升的小桶里，一定是放在9升的大桶里边。所以前一步需要做什么呢？为了只剩下6升的水，需要从9升的大桶里倒出3升的水。

那再前一步需要怎么样呢？为了能倒出3升的水，需要4升的小桶里先有1升的水。

那怎样能有1升的水呢？再看一眼题目，大桶9升，小桶4升，9升减4升再减4升，正好就是1升。

你看，这道题就解出来了，咱们再把逆向思维转化为正向操作， 第一步，大桶装满9升，倒进小桶4升，然后把小桶里的水倒掉。第二步，把大桶里的水倒进小桶4升，然后把小桶里的水倒掉。第三步，把大桶里剩下的1升倒进小桶，再把大桶装满水。第四步，用大桶的水把小桶倒满，大桶里就剩下6升。

你看，反过来想，这道题的思路就变得明确了。我们都玩过迷宫，从入口进去，想要找到出口，非常麻烦。可是如果把迷宫画到纸上，这件事儿就能变得简单，因为你可以倒过来思考，从出口出发，寻找去入口的路线，这种逆向思维，往往就能简单很多。

既然是谈寻找思路，我们还是要聊一下灵感这件事儿。其实波利亚并没有完全否定灵感，他也承认，如果你能产生灵感，对于你解题当然是有帮助的。关键在于，不能迷信灵感，要用一种更淡然的态度去面对它。

比如当你找到一个灵感，最后发现这个思路走不通。那也不必气馁。因为你在寻找思路的过程，常常是一个试错的过程。

你的猜想可能是错误的，但这样的猜想通常至少会包含真理的一个片段，当然它们也很少会揭示全部的真理。然而，如果你对一个猜想进行适当的检验，那么你还是有机会提炼出一个真理来。许多情况下，猜想结果被证明是错误的，但它对于启发一个更好的猜想还是有用的。除非我们不加甄别，否则，任何一个猜想都不会是没用的。

一个错误的思路，并不代表没有价值，根本没有想法才是真正糟糕的。

还有一个工具，也能成为你获得灵感的催化剂，就是刚才我们在聊如何理解题目时，一直强调的，盯住未知量。

盯住未知量这个事儿，强调多少遍都不算过分。

为什么呢？因为盯住未知量，你在解题的过程中，就能时刻记住你的目标到底是什么。莱布尼茨曾经有一个比喻，人的解题思考过程，就是一个晃筛子的过程，脑袋里边的东西都抖落出来，然后正在搜索的注意力就会抓住一切细微的、与问题有关的东西。

而你的注意力怎么能抓住和题目相关的东西呢？靠的就是未知量。未知量就像是一张通缉令，让你的注意力成为敏锐的侦探，可以从无数个念头中抓出来那个嫌疑人，否则，即使关键的东西抖落出来了，也可能没注意到。

靠着前边这些方法，咱们理解了题目，找到了思路，根据这个思路，我们就能解出一个答案。可是接下来还是会面临一个问题，怎样确定自己这个答案是不是正确的呢？

如果你做的是练习册，那就很简单了，翻到最后一页对答案呗。可是，如果是实际问题，没有标准答案，那怎么验证呢？

你可以从两方面验证你的解答。

如果是物理问题，或者是几何问题，有一个非常好用的工具，叫「量纲检验」。

什么叫量纲呢？就是长度、面积、重量的那个标准单位。很多物理问题或几何问题，我们求出来的往往是个表达式，之后怎么样快速检验呢？就把表达式每一项的单位代入进去，看看两边是不是相等。

比如用我们都知道的，长方体的体积公式，V=abc，左边是体积，单位是立方厘米；右边a、b、c分别是长、宽、高，单位都是厘米，乘在一起就是立方厘米。这么一对照，两边都是立方厘米，这个答案就比较靠谱。

另一种验证的工具，叫做「特殊化」。

简单来说，就是你求出了一个公式，那么我们可以用具体的值来验证。

比如还是长方体的体积公式，我们就可以用一个具体情况，长宽高都是1厘米，我们知道体积就是1立方厘米。代入到公式中，算出来果然也是1立方厘米。

所以，量纲检验和特殊化，其实可以组合起来用，如果你的解答有问题，用这两种检验方式，往往就能快速发现错误。

到这里，我们理解了题目，找到了思路，完成了解答并且验证无误，看起来，解题的任务就算胜利完成了。但是波利亚告诉我们，别着急，最后还有非常重要的一步，那就是回顾。

你可能会问，找到答案就完事儿了，为什么还要回顾呢？

因为解题不止为了找到答案，更是反思解题过程中的一般性的、跨问题的思维法则，简单来说，是为了找到可复用的方法。

简单地将题目解出来，只能得到很少的东西，如果解不出来，看一眼答案，觉得自己恍然大悟了，那只能得到更少的东西。如果没有反思，就不能抽取出一般性的东西应用到更多的题目上去。

那怎样做回顾呢？波利亚列出了一张清单，帮助你从不同的方面考虑你的解答，并寻找与你过去所获知识之间的联系。

你可以考察解答中那些比较冗长的部分，看看能不能使它们变得简短些；

你可以重新审视题目，看自己能不能一眼就能看出整个解答；

你可以对你的解答进行改进，看看能不能让它更直观；

你可以重新审视题目，看看是哪个细节让你产生了关键的思路；

你还可以仔细检查你的结论，看看这个结论能不能应用于别的题目。

在回顾的过程中，你也许能找到一个更好的新解答，找出新的有趣的事实。就算没有，如果你养成了以这种方式回顾和仔细检查你的解答的习惯，你将会获得一些条理分明、随时可以使用的知识，并且将会提高你的解题能力。

这本书中有一句名言：「方法和手段有什么不同？方法就是你用了两次的手段。」

只有经过主动的回顾，你才可以把解题过程中用到的有创造性的手段，变成未来可以重复使用的方法。

到这里，这本《怎样解题》其中精华的部分，我就为你解读完了。

总结一下，我们重点谈到了解决问题时，四个关键的步骤：

第一步，熟悉题目并且理解题目。尤其要抓住未知量，因为抓住了未知量，就是锚定了你的目标。

第二步，了解已知数据和未知量之间有什么关系，寻找解题的思路，也就是为自己拟定一个方案。

其实在此之后还有一步，那就是执行方案，不过在解决数学问题的时候，我们往往卡在寻找思路上，一旦找对思路，执行方案就是水到渠成。

第三步，验证你得到的答案，确认它是否正确。

别忘了关键的第四步，回顾，只有经过主动的回顾，你才可以把解题过程中用到的有创造性的手段，变成未来可以重复使用的方法。

其实这本书中除了介绍这些方法，波利亚对于另一个话题的讨论，也让我感觉非常惊讶。

那就是解决问题的决心。

波利亚说，把解题作为是纯粹的「智力活动」是错误的，决心和情绪也起了很重要的作用。要解决一个重大的科学问题，只有靠毅力才能坚持长年累月的艰苦工作，忍受痛苦的挫折。

我们总把突然而来的好念头看成一种灵感，一种上帝的恩赐。你必须努力工作，或者至少有强烈的愿望求解题目，才配得到这种恩赐。即使是所谓灵感，也来源于勤奋和专注。

那么这种决心和意志力是与生俱来的吗？一部分是，另一部分，其实可以靠科学的方法来补充。聪明的解题者，会规划自己的展望，不止追求最终的成功，还会在中间设置小的节点，每完成一个节点，就获得了一次小的成功，这个时候，就更有决心继续下去。

你看，面对难题，不论是一开始拥有靠谱的方法，还是拥有巨大的决心，解决问题的高手，总能是让决心和方法能成为一个闭环：用决心推动方法，靠方法获得突破，借助突破坚定自己的决心。

这，才是解题高手的终极心法。

撰稿、转述：陈章鱼 脑图：摩西脑图工作室

划重点

1. 我们平时所说的洞察力、判断力、创造力、思维能力等，其实可以通过不断模仿和实践解题技巧来提高。

2. 理解题目时，尽可能清晰、生动地使整个题目形象化。

3. 一个错误的思路，并不代表没有价值，根本没有想法才是真正糟糕的。

4. 只有经过主动的回顾，你才可以把解题过程中用到的有创造性的手段，变成未来可以重复使用的方法。

5. 用决心推动方法，靠方法获得突破，借助突破坚定自己的决心。