《费马大定理》 柴知道解读

《费马大定理》| 柴知道解读

关于作者

西蒙·辛格，剑桥大学粒子物理学博士，BBC 导演，英国电影和电视艺术学院奖的最佳纪录片奖获得者。

关于本书

《费马大定理》是西蒙·辛格深入采访了费马大定理的证明者——安德鲁·怀尔斯之后所写就的作品，中文版曾获得“全国优秀科普作品奖”。辛格所执导的同名纪录片获得了英国电影和电视艺术学院奖的最佳纪录片奖。

核心内容

本书以费马大定理为线索，穿插介绍了数学的发展史，并详尽地记录了费马大定理的诞生过程，数学史上围绕它的种种传奇故事，以及安德鲁·怀尔斯激动人心的奋斗历程。

你好，欢迎每天听本书。本期音频为你解读的是《费马大定理》，副标题是“一个困惑了世间智者358年的谜”。这本书的中文版大约23万字，我会用大约29分钟的时间，为你讲述书中精髓：数学家是如何证明费马大定理的？

我先来说一说什么是费马大定理。费马大定理又被称为“费马最后的定理”，其实它很简单，就是说当整数 n >2 时，x^n + y^n = z^n 这个方程，没有正整数解。

从这本书的副标题“一个困惑了世间智者358年的谜”，我们就能看出来，费马大定理是全世界最为出名的数学难题之一，它的诞生也颇富传奇色彩。费马是17世纪的一位天才数学家，费马大定理，其实只是他在一本书的页边空白处写下的一句话而已。好玩的是，费马写下这一定理之后，又加上了一句数学史上最著名的批注，“我有一个对这个命题非常美妙的证明，但这里空白太小，我写不下。”

只要了解一点数学常识的人都知道，既然叫费马大定理，那就说明，它已经被证明了是成立的。在没被证明之前，就只能叫猜想，成不成立还不一定。虽然费马自称证明了费马大定理，但是其他数学家们并没有在费马的手稿中发现证明过程。不光如此，历代数学家们前赴后继，也没能证明费马猜想是对的，所以猜想只能是猜想。直到1995年，数学家安德鲁·怀尔斯完成了证明，费马猜想才终于变成了费马大定理。顺便说一下，这个“大”字，也不是随便加的，它是为了区分于另一个叫做费马小定理的数学定律。

你可能会想，数学本来就很抽象了，数学家们花了几百年都证明不了的费马大定理，我们普通人怎么能听懂？的确，像黎曼猜想等著名的数学问题，普通人的确是连符号都看不懂。但费马猜想不一样，它一方面非常简单明了，初中生都能听懂，但另一方面，想要证明它却难如登天。今天要讲的《费马大定理》这本书，讲述的就是数学家们证明费马大定理的故事。以费马大定理为线索，书中穿插介绍了许多精妙的数学思想，可以说是一部简写的数学发展史，非常精彩。看这本书的感觉，一点都不像是在读科普，而是像在读小说或者看电影，让人欲罢不能。有书评说，这本书围绕着一个难度极高的谜题，讲了一代代数学精英在这个谜题上的前仆后继，最终出现了一位天才，经过7年的秘密奋斗，最终征服了这个千古难题，再次验证了数学之美。整个故事结构就像好莱坞电影一样，非常激动人心。

为了展现证明费马大定理这段历史的精彩之处，接下来，我就顺着原书思路，从三个角度来为你介绍本书精髓：第一个问题，费马大定理为什么这么出名；第二个问题，数学界是怎么研究费马猜想的；第三个问题，安德鲁·怀尔斯是如何证明费马大定理的。

先来看第一个问题，费马大定理为什么这么出名？

费马1601年出生在法国，他的父亲是一位皮革商，很有钱，费马从小也受到了很好的教育。不过费马并不是一位职业数学家，他的本职工作，其实是一位高级公务员。不过费马这个人没有什么政治野心，而且当时的政治局势也比较混乱，费马不想趟浑水，所以把自己的业余时间全都用在了数学上。从这个角度来说，费马其实是一位业余数学家，但他在数学上实在是太有天赋了，所以被称为“业余数学家之王”。

那费马对数学的发展做出了哪些贡献呢？费马是概率论的创始人之一，他和同时代的数学家帕斯卡，共同创立了概率论，这是现代数学中一个极其重要的分支。此外，费马还对微积分的创立做出了很大的贡献。一直以来大家都认为，微积分是牛顿发明的，但1934年的时候人们发现，牛顿自己在笔记中说，他是在费马关于切线的研究的启发下，才发展出了微积分。

光是凭借着对概率论和微积分的贡献，费马就足以进入数学名人堂了。但费马最大的成就，还不是概率论和微积分，而是在数学的另一个分支，“数论”上。数论研究什么呢？其实就是研究数字，以及不同数字之间的关系，就是一个纯粹的智力游戏，所以数论也被认为是最纯粹的数学。著名的数学家高斯曾说，“数学是科学的皇后，数论是数学的皇后”。数论在数学中的地位，由此可见一斑。

费马大定理，就是数论中的一个著名的难题。这条定理是怎么来的呢？大约是1637年，费马在看一本叫做《算术》的数学书。当时费马正在看勾股定理，也称为毕达哥拉斯定理，这条定理是这样的：可以找到三个整数 X、Y、Z，让 x^2+y^2=z^2。比如说，3的平方加4的平方等于5的平方，那么3、4、5就满足这个条件。你可以一直往下找，满足这个条件的整数组无穷无尽。

费马看到这里的时候，灵光一闪，那么有没有可能找到三个整数，让 x^3+y^3=z^3 呢？如果不是3次方，而是4次方呢，有没有可能找到三个整数，让 x^4+y^4=z^4 呢？费马把这个想法写在书的空白处。

费马认为，这样的数字并不存在。我们不可能找到三个整数，让它们满足 x^3+y^3=z^3。而且不光如此，你把3次方换成4次方、5次方、6次方，直到 n 次方，都不可能。只要 n 大于2，x^3+y^3=z^3 的方程，就没有正整数解。这个就是著名的费马猜想。

费马在书的页边空白处写下了这个猜想，然后又写了一句批注，说我已经找到了一个证明方法，但这里空白太小，我写不下。这句话看起来很像恶作剧，但其实是费马一贯的风格。跟很多其他的数学家不一样，费马只喜欢叙述定理，但不喜欢证明定理。他经常写信给其他数学家，说又发现了一个什么定理，但是他却不提供详尽的证明，最多也只是用非常简略的步骤随便证明一下，对方压根就看不懂。

费马之所以这么做，除了带有一点恶作剧的成分以外，也有非常实际的动机。因为证明一个定理很难，需要花费大量的时间去寻找各种各样的方法，而且给出证明以后，还要接受来自同行的严格检验，一旦出现任何一个漏洞，就前功尽弃了。所以费马的选择就是，我不提供完整的证明，尽量把时间省下来，广撒网，投入到其他的问题中去。

费马猜想乍看上去并没有什么特别的，那为什么那么出名呢？这就是因为，要想证明费马猜想，可以说是难如登天。费马人生中提出的大大小小各种定理，后来都一个一个地被证明了，唯有费马大定理，一直无法解决，所以它也被称为“费马的最后定理”。有数学家悲观地认为，也许在人类文明消亡之时，费马猜想也无法被解决。

费马猜想的名声之大，甚至已经超出了数学界。比如有人在小说中设置了这样的情节，说一个人和魔王做交易，他要问魔王一个问题，如果能把魔王难住，那就能获得十万美元；如果魔王在24小时之内破解了这个问题，那他就要出卖自己的灵魂。这个人问魔王的问题就是：费马猜想到底是不是正确的？魔王听完之后，风驰电掣地跑遍全地球，吸收了所有的数学知识，甚至还跑到其他星球上寻找外星数学家的帮助，最终也没能解决这个问题，只好认输。从这个角度上来说，当时“费马猜想”已经成了“难题”的代名词。

以上分享的就是今天的第一个问题，费马大定理如此出名的原因。下面，我们回顾一下这部分的内容。费马大定理的内容很简单，当整数 n >2 时，x^n + y^n = z^n 这个方程，没有正整数解。费马大定理出名的原因，一方面是因为它的诞生非常富有传奇色彩，另一方面，也是因为要证明它的难度极高，对人类的智慧形成了重大的挑战。

在第一部分，我们说完了要想证明费马猜想难度极高，那么第二个问题我们就要来看一下，数学家们对于费马猜想这个难题的研究过程是怎样的。

前面讲到，费马自己在书的空白处写了，我已经找到了一个绝妙的证明，但是书边的空白太小，写不下。那么你可能会想，是不是说，其实光凭费马那个年代的数学知识，我们就可以证明费马猜想了呢？我们的确无法排除这种可能，即使真是这样，那这种证明方法也实在太难想了，许多数学史上的天才，都没能证明费马猜想。

举个例子，18世纪伟大的数学家欧拉，在数学史上具有极其崇高的地位，是现代数学的奠基者之一，我们现在说的“函数”的概念，就是欧拉最早提出来的。就是这样一位数学天才，也曾经试图证明费马猜想，但最终却失败了，我们来看看他是怎么做的。

费马猜想说，x^n + y^n = z^n，当 n 大于2的时候，这个方程没有整数解。欧拉就想，可以先给 n 找一个特殊值，比如说3，然后证明在 n=3 的情况下，费马猜想是成立的。有了这个基础之后，我再把这个结论推广开来，推广到4、5、6、100、1000……直到无穷，就可以证明费马猜想了。这个方法有点像是多米诺骨牌，只要先推倒第一块，剩下的牌就都倒了。

欧拉的这个想法的确高明，而且更幸运的是，他还找到了费马自己所留下的一个证明。他在翻阅费马手稿的时候发现，费马在《算术》那本书里的另一个地方，证明了当 n=4 的时候，费马猜想是成立的。而且，虽然费马的证明过程非常简略，但是其中却透露出了一种方法，叫“无穷递降法”。有了这第一块多米诺骨牌，事情就好办多了。

欧拉利用费马的证明结果和方法，再开创性的引入了“虚数”的概念之后，成功地证明了，当 n=3 的时候，费马猜想也是成立的。这是在费马自己的证明之后，数学家们在费马大定理上取得的第一个突破，非常伟大。但问题是，虽然证明了费马大定理在 n=3 和4的时候成立，但欧拉设想中的，像多米诺骨牌那样的结果，并没有出现。对这两个特殊数字的证明结论，无法推广到其他情况中去。所以即使是伟大的欧拉，也在费马猜想这个问题上失败了。

之后又有一些杰出的数学家在欧拉的基础上继续前进，也取得了巨大的成就，但也只能证明费马猜想在某些特殊数值中是成立的，没人能完整地证明费马猜想。到了20世纪之后，新一代的数学家们已经不研究费马猜想了，因为这个问题已经被公认为几乎不可能解决，大家不想浪费时间，就都去忙着研究其他领域的数学知识了。

但到了20世纪后半期，一种新的、威力强大的新技术出现了，这就是计算机。计算机技术的出现，意味着计算量不再是一个问题，我们可以通过大量的计算来暴力解决很多难题。不光如此，计算机还能给数学家们提供了很多解决问题的新思路，这就像是 AlphaGo 和柯洁下棋一样，AlphaGo 所采取的很多下棋策略，也可以给人类棋手带来巨大启发。

在数学中，计算机也能带来相同的效果。比如说“四色定理”的证明，就是依靠计算机完成的。四色定理是说，任何一张地图，不管是什么形状结构，都只需要四种颜色上色，就可以保证任何两块相邻区域的颜色都不同。数学家们研究了很久，最终是依靠计算机才完成了证明，而且，目前还没有除了计算机以外的证明方法，由此可见计算机的强大，以及它对数学发展的推动。

在二战之后，数学家开始用计算机技术来处理费马猜想。到了20世纪80年代，数学家已经通过计算机证明，当n小于25000的时候，费马猜想都是成立的。那我们能不能由此推断出费马猜想就是对的呢？很可惜，不行。数学定理的证明，只能建立在逻辑论证的基础上。即使你证明了费马猜想在 n 小于100、10000、100万的时候都成立，从逻辑上来说，你也不能保证 n 在100万加1的时候也成立。即使你通过计算机把 n 的值不断提高，费马猜想能不能成立，也还是个未知数。

那你可能会说，这不是在抬杠吗？还真不是。举个例子，大数学家欧拉也提出过一个欧拉猜想，说  x^4+y^4+z^4=w^4 这个方程不存在正整数解。200多年以来，人们既无法证明欧拉猜想，也找不出反例，但在1988年的时候，哈佛大学的一位数学家真发现四个整数，能满足欧拉说的那个方程，也就是说，欧拉猜想由此被证伪了，不成立。

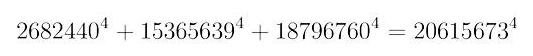
所以这也说明，即使一个猜想在10万、100万以内都成立，我们也无法保证它就是正确的。也就是说，无论计算机多么强大，通过庞大的计算把 n 的值提高到多大，在没有进行严谨的逻辑证明之前，我们都不能说费马猜想是一定成立的。

不光如此，随着数学的发展，费马猜想还面临着另一个更为诡异的情况。1931年的时候，数学家哥德尔提出了一条划时代的著名定理，叫“哥德尔不完备性定理”。这一定理是数学上和逻辑学上的里程碑，因为它意味着，数学家并不一定能解决一切数学问题，有可能存在着某一条定理，它的的确确是对的，但却永远也无法被证明，也无法被证伪。既然如此，人们理所当然地会想，费马大定理，是不是恰好就是一条这样的定理？一代又一代顶尖的数学家们都没能解决这个问题，或许不是因为他们水平不够，而是因为这条定理从本质上就是不可被证明的。如果真是这样的话，那费马猜想就永远不可能被解决了。

以上分享的就是第二个问题，数学家对费马大定理的研究。下面，我们来回顾一下本部分的内容。像欧拉这样的顶尖数学家，都只能证明在某些特殊的情况下，费马猜想是成立的，但却无法完整地证明费马猜想。即使到了现代，在计算机技术的帮助之下，数学家们还是没能解决这一问题，只能把费马猜想的成立范围不停的扩大而已。根据“哥德尔不完备性定理”，有可能存在着一个永远不可能被证明的定律，这就更为费马大定理的解决蒙上了一层阴影。

刚才讲到了，一代又一代的数学家，加上计算机技术，都没能解决费马猜想。那现在就要来看看今天分享的第三个问题，安德鲁·怀尔斯是怎么解决这一难题的。

安德鲁·怀尔斯1953年出生在剑桥，是一位英国数学家。在怀尔斯10岁那年，他跑去当地的社区图书馆里看书，无意中看到了一本专门讲述费马猜想的书。怀尔斯自己说，历史上所有的大数学家都没能证明费马大猜想，但与此同时，费马猜想又如此简单而美丽，一个10岁的孩子都能看懂。所以从那一刻起，他就被费马大定理深深吸引住了，立志要解决这个问题。这不是空想，当时小怀尔斯阅读了许多关于费马猜想的资料和论文，并尝试去解决它，当然了，没能成功。

1975年，怀尔斯开始在剑桥大学读博士。在之前的十年中，怀尔斯一直心系费马猜想。但在读博士之后，他却不能再一门心思专攻费马猜想了，这跟当时数学领域的实际情况有关：在当时看来，费马猜想虽然很出名，难度也很高，但在数学领域却并不算很重要。

为什么这么说呢？从判断一个数学问题的是否重要的角度来看，费马猜想适用范围很窄，又不能带来新的数学知识，而且也不处于数学研究的基础位置。从这几个标准来判断的话，实话实说，费马猜想并不是很重要。西蒙·辛格做了一个比喻，说在很长一段时间内，费马猜想在数学界的地位，就相当于炼金术在化学界的地位，虽然很富有传奇色彩，但却被认为是不切实际的，很少有人去研究它。

怀尔斯自然也明白这个道理，所以决定暂时把费马猜想搁置一下，去研究一些更有意义的数学问题。怀尔斯的导师为他选定了一个研究方向，叫“椭圆曲线”，这也是当代数学领域一个非常重要的问题，怀尔斯此后就在这个领域精耕细作，并且成为了这个领域的著名专家。

本来怀尔斯可能跟费马猜想无缘了，但到了1984年，情况突然峰回路转。当时一群数学家在德国召开了一个学术会议，其中有一位叫弗莱的数学家提出，椭圆曲线研究领域里的一个猜想，叫“谷山-志村猜想”，跟费马猜想有密切的关系。他提出，如果能证明谷山-志村猜想，那费马猜想也就自动得到了证明。这就意味着，数学家们不用去直接面对费马猜想了，只要证明谷山-志村猜想，费马猜想就会迎刃而解。

当然了，谷山-志村猜想也是一个非常非常难以证明的问题。当时这个猜想也已经提出了30多年，很多数学家都不愿意去证明它，因为难度极高。但与此同时，谷山-志村猜想又是一个意义重大、价值很高的问题，一旦被证明，就可以极大地推动数学的发展。

为什么这么说呢？这也跟数学研究的特点有关。在数学研究中，不同的领域，就像是海上的一个个孤岛，有数学家专门研究几何，也有数学家专门研究概率，不同领域之间相互隔绝，研究几何和研究概率的人，可能基本上没什么交流。而谷山-志村猜想，就是在两个看起来毫无关系的数学领域，也就是“椭圆曲线”和“模形式”之间，搭起了一座桥梁。这种桥梁的价值是非常高的，它能让不同的数学研究领域之间相互融合，解决很多以前根本无法解决的难题。当代数学中最恢宏的一项计划，叫“朗兰兹纲领”，就是试图在不同的数学领域之间搭建起桥梁，形成一个大一统的数学。所以说，谷山-志村猜想的研究价值是非常高的。这从数学界当时的论文状况中也能感受到，许多数学家都会在论文中说，假如谷山-志村猜想是正确的，那么我就能解决什么问题，得到什么什么结论，一大堆成果，都建立在这个猜想的基础之上，所以一旦谷山-志村猜想被证实，就能极大地推动数学的发展。

言归正传。1986年，怀尔斯听到了弗莱的研究成果，内心受到了极大的震动，非常兴奋。因为他的研究领域恰恰就是椭圆曲线，现在居然出现了这样的机会，可以直接把他的研究领域和费马猜想挂上钩，更何况谷山-志村猜想又如此有价值，这等于给了他一个研究费马猜想的天赐良机。所以怀尔斯立刻决定，要证明费马猜想，实现自己的童年梦想。

从1986年开始，怀尔斯开始独自一人，秘密研究费马猜想。这种秘密研究的方式，其实跟数学界的主流是背道而驰的。一般来说，数学是没有秘密的，大家经常相互交流想法，而且如果自己的想法有什么问题，也可以在交流中得到纠正，防止走进死胡同。独自研究一个难题风险很大，即使哪里错了，都不会有人来提醒纠正。

但为了避免研究成果被他人获得，抢走证明费马猜想的荣誉，怀尔斯最终决定在自家的阁楼上独自研究。在长达7年的时间里，除了自己的妻子以外，没人知道怀尔斯到底在研究什么。为了掩饰自己的工作，怀尔斯每隔半年会发表一篇小小的论文，这样既不会暴露自己真正研究的问题，也不会让同行觉得自己脱离学界，行为异常。在7年的时间里，怀尔斯尝试了各种办法，苦心计算，深入到整个数学大厦中最黑暗最幽深的角落，试图证明谷山-志村猜想。怀尔斯所经历的种种艰辛和挣扎，外人恐怕很难理解，他几度山穷水尽，最终又柳暗花明。

终于，到了1993年，安德鲁·怀尔斯完成了证明，并且在自己的家乡剑桥，发表了关于费马大定理的世纪演讲，轰动了全世界。《纽约时报》等顶级媒体都把这条新闻作为头版头条来报道，怀尔斯一夜之间成了全世界最出名，可能也是当时唯一出名的数学家。

怀尔斯对于费马大定理的证明，是由几千个逻辑链构成的特大型论证，涉及到古往今来的各种数学方法，极其艰深，一共分6章，整整200多页，一般人根本看不懂。普通的数学论文要发表在顶级期刊上，一般需要2到3个审稿人来检查，但怀尔斯的证明，需要6个审稿人共同审查，堪称是最为严格的学术检验。结果发现，怀尔斯论文的其中一章有一个小问题，这个问题初看简单，但随着时间推逝，怀尔斯却发现，这其实是一个关键的致命伤。按照怀尔斯一位同事的说法，这个问题就像是在房间里铺地毯，虽然几乎所有的地方都已经铺的平平整整了，但总有一小块地方会鼓起来。如果你非要把这块地方按平，那又总会有另外一个地方出现问题。

在这个问题被提出后，怀尔斯立刻开始了补救，但花了整整一年的时间，怀尔斯还是没能解决这个问题。而且怀尔斯知道，证明费马大定理的荣誉，只属于最终证明它的那个人，即使怀尔斯做出了最大的贡献，如果他不是第一个完成完整证明的人，那这份荣誉仍然与他无关。因此，怀尔斯始终拒绝公开手稿，坚持由自己来解决这个问题。这么一来，外界对于他的质疑也达到了顶峰。

但14个月之后，情况突然峰回路转。就在怀尔斯准备承认失败之时，他奇迹般地发现了一个解决方法，成功地补救了自己的证明。1995年，怀尔斯把证明过程发表在了《数学年刊》第142卷，如此一来，证明费马大定理的荣耀，终于彻彻底底地归属于怀尔斯了。他的工作还带来了许许多多开创性的数学方法，极大地推动了数学的进步。

以上就是今天分享的的第三个问题，安德鲁·怀尔斯是如何证明费马大定理的，我们来回顾以下这部分的内容。怀尔斯从小就对费马大定理感兴趣，在成为职业数学家以后，他恰好发现自己的研究领域跟费马大定理相关，于是开始了长达七年的秘密研究。之后又经历过一次长达一年的修改之后，怀尔斯终于证明了费马大定理，在此过程中还创造了许多有用的数学技术，极大地推动了数学的发展。

讲到这里，《费马大定理》这本书的精髓，也就是数学家们是证明费马大定理的故事，你就有所了解了。我再来为你总结一下。

首先讲到的第一个问题是，费马大定理为什么如此出名？费马大定理看起来很简单，就是说当 n＞2 时，x^n + y^n = z^n 这个方程，没有正整数解。但要证明费马大定理却难如登天，它对人类的智慧提出了重大挑战。此外，费马大定理的诞生也非常有传奇色彩，它是费马在书的空白处随手写下的一个定理，还附加上了一句有恶搞成分的批注。

接着讲到的第二个问题是数学界对于费马大定理的研究。像欧拉这样的顶尖数学家，都曾尝试证明费马大定理，但都没能成功，只能证明费马大定理在某些特殊情况下是成立的。到了20世纪，计算机技术的诞生极大地推动了数学界的发展，但却同样无法证明费马大定理。

最后一个问题讲到了，安德鲁·怀尔斯是如何解决费马大定理的。怀尔斯的研究领域是“椭圆曲线”，随着数学的发展，他发现自己的研究领域跟费马大定理产生了联系，于是决心解决这一问题。在经历了长达7年的秘密研究，和1年多的修改之后，怀尔斯成功证明了费马大定理，对数学的发展做出了极大的贡献。

看完这本书，我有一个感受。我们平常可能会认为，数学家或科学家这样的群体，只对真理感兴趣，对金钱荣誉无欲无求。但如果多了解一些学术史的话就会发现，即使是牛顿、怀尔斯这样的顶尖学术天才，也会用尽手段，来为自己争取荣誉，希望能在学术史上留下自己的名字。这种心态，其实完全是一种正常的人性，没什么好羞愧的。而且正是这种对荣誉的追求，才促使着一代又一代的天才们去探寻真理，推动人类的进步。

撰稿：柴知道 脑图：摩西 转述：江宁

划重点

1.费马大定理看起来很简单，但要证明费马大定理却难如登天，它对人类的智慧提出了重大挑战。

2.顶尖数学家，都曾尝试证明费马大定理，但都没能成功，计算机技术的诞生同样无法证明费马大定理。

3.怀尔斯发现自己的研究领域跟费马大定理产生了联系，在经历了长达7年的秘密研究，和1年多的修改之后，他成功证明了费马大定理.