《深奥的简洁》  陈章鱼解读

《深奥的简洁》| 陈章鱼解读

关于作者

约翰·格里宾，是剑桥大学天文物理学博士，也是一位畅销书作家，著有50多部科普著作。2009年，格里宾被英国科学作家协会授予「终身成就奖」。

关于本书

这本书是混沌理论的经典科普书，通过对各种复杂与混沌案例的分析告诉我们，整个世界都建立在简单的元素之上，它们经由互动与组织，便可造就出高度复杂的整体。

核心内容

音频聚焦在三个重要问题：

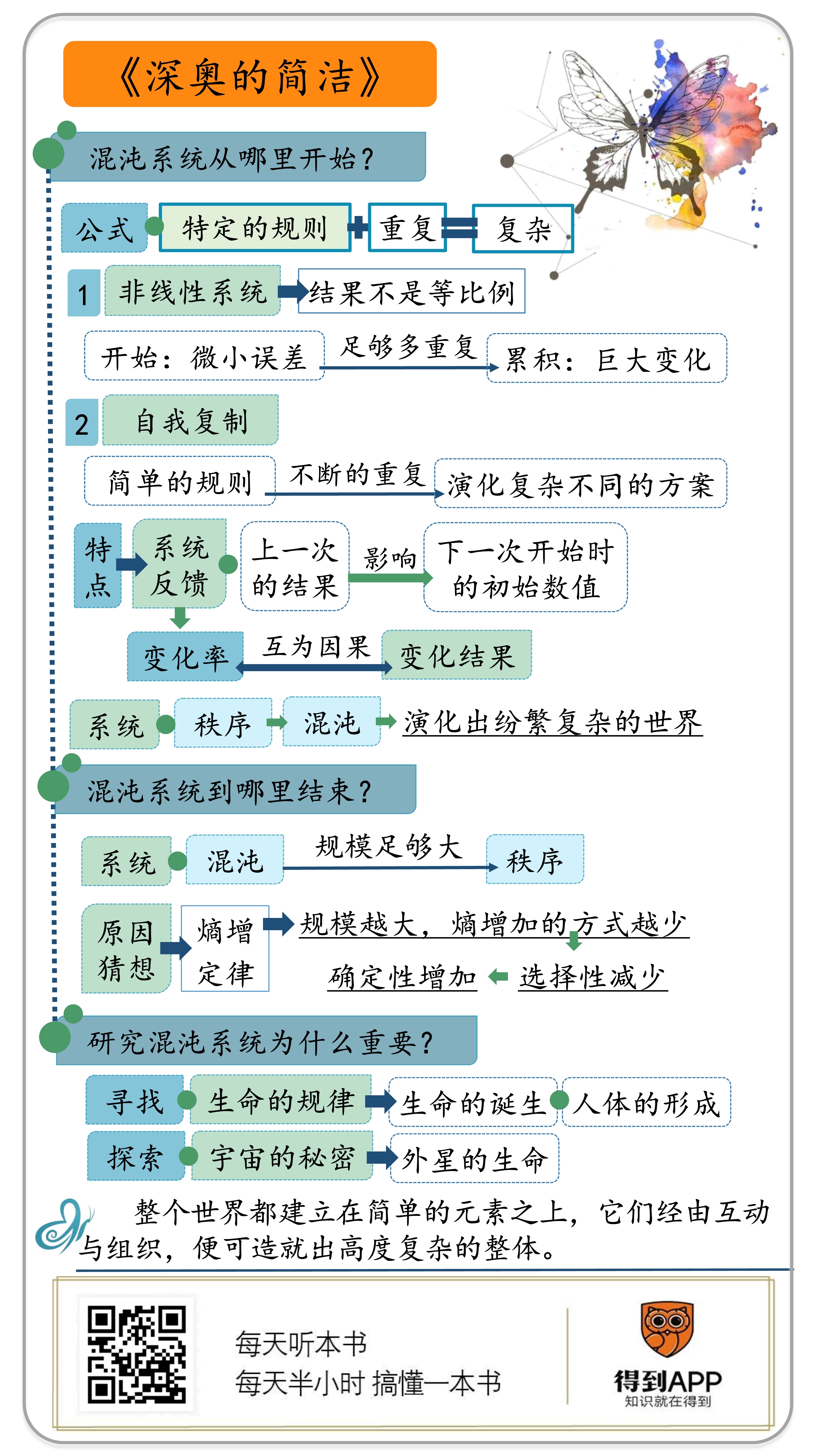
1.混沌系统从哪里开始？

2.混沌系统在哪里结束？

3.研究混沌系统为什么这么重要？

你好，欢迎每天听本书，我是陈章鱼。今天为你解读的这本书叫《深奥的简洁》。这本书讲的是，复杂的混沌系统背后，到底有什么样的规律？

对于混沌系统，你一定不会陌生，哪怕你没听过「混沌系统」这个概念，你也一定听过那个最具代表性的事例——蝴蝶效应。

1961年，美国的一位气象学家爱德华·罗伦兹在研究气流运动，他发现，用计算机进行计算的时候，哪怕是小数点之后第 4 位数有那么一点不一样，也就是差那么万分之几，算出来的结果就完全不同。后来罗伦兹把这个现象进行了一个形象的比喻，说这就像是巴西的一只蝴蝶扇动翅膀，就可能引发美国得克萨斯州的一场龙卷风。

从此之后，「蝴蝶效应」也就成了混沌系统的代名词。不过，如果我们再往深处想一层，你会发现关于蝴蝶效应，有很多问题我们是不了解的。

比如，蝴蝶效应指的是，微小的变化会引发的巨大反应，那么多微小的变化，才会产生蝴蝶效应呢？蚂蚁搬家会不会产生这样的效果呢？云朵中的一滴水落下来，有没有可能呢？

更关键的，巴西的一只蝴蝶能引发得州的一场龙卷风，那得州的龙卷风为什么没有引发全美的海啸呢？这说明混沌系统到了一定的规模，它就又开始有规律了，不会一直这么混沌下去。

所以你看，我们用常识来推断，也能得出这样一个结论，就是混沌系统是有边界的。就像是有一个圈，这个圈里边就是混沌系统，变化无常、难以预测，而圈子之外，就是秩序所在。

有人说，这本书的书名不应该叫《深奥的简洁》，其实应该叫作《蕴含于复杂中的简洁》。因为这本书探讨的，就是混沌和秩序的边界到底在哪里。

这本书的作者约翰·格里宾，是剑桥大学天文物理学的博士，也是一位畅销书作家，著有50多部科普著作。2009年，格里宾被英国科学作家协会授予「终身成就奖」。他在这本书中，就通过对各种复杂与混沌案例的分析告诉我们，整个世界都建立在简单的元素之上，它们经由互动与组织，便可造就出高度复杂的整体。

接下来，我会分成三个部分为你解读这本书。

第一部分我们来看看，混沌系统从哪里开始？

第二部分我们来了解一下，混沌系统到哪里结束？

第三部分我们再来聊一聊，研究混沌系统为什么这么重要？

我们来看第一个问题，混沌系统从哪里开始？

一般我们会以为，混沌系统如此难以预测，它的内部也一定非常非常复杂，一定是内部环节众多，就像一台零件特别多的机器，因为环节多、零件多，所以内部的变数就多，最终的结果就难以预料。

实际上，想要制造出一个混沌系统，根本不需要那么复杂。其实，我们随手就能制造一个混沌系统，只需要一件东西，那就是水龙头。

你可以拿水龙头做这样一个实验，先把水龙头关紧，然后打开一点点，这时候的水，是一滴一滴落下来的，嘀嗒、嘀嗒，节奏感特别强。你再把水龙头打开一些，水滴就会越来越快，最终汇成一股水流。如果你再把水龙头打开一些，这个时候有趣的事情发生了，你会发现水流开始变得杂乱无章，也许还会分成几股。那如果你把水龙头继续开大，最后，这些水流又会汇成一股稳定的大水流。

如果你反复试验几次，你会发现，这是一个从规律到混乱又到规律的过程。不论你试验几次，一头一尾都是不变的，可是中间那个水流会变成什么样，这个完全是随机的，找不到什么规律。

中间这些混乱的水流，就是一个混沌系统。

所以你看，我们根本不需要那么复杂，就能随手造出一个小小的混沌系统。可见，内部结构是不是复杂，和混沌系统之间没有太多的关系。

那到底什么才是混沌系统的决定因素呢？这本书的作者提出了一个公式：特定的规则+重复=复杂。

就是一些看起来其实很明确简单的规则，经过多次重复之后，就会演化成一个混沌系统，结果变得难以预料。

那都有哪些规则呢？主要有两类。

第一类是「非线性系统」。日常生活中的大多数变化都呈线性发展，也就是等比例的变化。我举起一袋2公斤重的米，要比举起1公斤米花上两倍力气。我往前走200米，也要比走100米花上两倍的力气，都是这样等比例的。

线性系统是没法变成混沌系统的，因为线性系统里边的变化也好，误差也好，最终都会等比例地呈现在结果中，非常明确，也就不会变成我们无法预估的结果。

反过来，如果结果不是等比例的，那么它就是一个非线性的系统，这样的系统，如果开头有一点点微小的变化，结果就可能大不相同。

比如指数，也就是多次相乘，这就是一个非线性的系统。

网上有一个励志的段子，说我每天多努力一点点，提升1%，365天之后，结果是37.8倍；如果我每天少努力一点点，减少1%，365天之后，结果就是0.03。

你看，多1%和少1%，一开始不过是0.02的差别，但是放到这样一个非线性系统里，结果却差出了一千多倍。

像是我们前边提到的「蝴蝶效应」，研究气流运动的数学计算，也一定是一个非线性系统。如果你感兴趣，可以找一个计算器来，咱们通过一个简单的计算，也能模拟出「蝴蝶效应」那个计算的情况。

步骤非常简单，你先挑一个0到1之间的小数，小数点之后多取几位数，比如0.34567，然后进行三步的运算。

第一步，用计算器计算这个数的平方；第二步，将平方的结果乘以2；第三步，再将这个结果减去1。

接下来，你可以将这三步重复20次，记下最后得到的结果。

然后，请你把一开始选择的那个小数做一点点调整，比如把0.34567变成0.34563。然后再将那三步计算重复个20次，记下最后得到的结果。

把两个结果对到一起，你会发现，虽然只有0.0000几的变化，但是最后的结果大不相同。甚至有的时候，两个结果的正负都不一样。

其实呢，我们只用了一个简单的算式，那就是2x2-1。只不过，这是一个非线性的计算，经过足够多的重复之后，一开始的微小误差，就会累积成巨大的变化。

还有第二种规则，也能创造出混沌系统，就是「自我的复制」。

比如数学当中有一类几何图形叫作「分形」，就是通过自我复制的方式，产生的图形。最著名的分形叫作「科赫曲线」。

科赫曲线的绘制规则非常简单，先取一条线段，把它三等分，然后在中间的线段向外突出一个三角形。之后，对每一条新产生的边重复这个操作，以此类推，以至于无穷。

我在文稿中附上一张图，你能看出来，经过几次重复之后，虽然绘制的规则非常简单，但是得出的曲线已经非常复杂了。

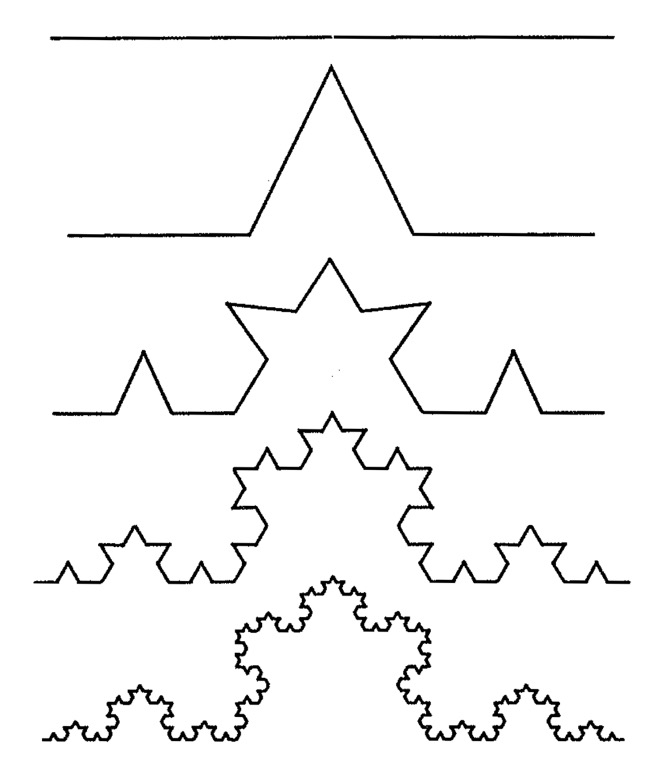
如果一开始选择的线段长度不同，那么最后得到的科赫曲线也不一样，可以说能衍生出无数种可能。

你可不要小看科赫曲线，比如岛屿的海岸线，看起来弯弯曲曲，哪儿和哪儿都不一样，但是实际上，经过科学家的研究，自然形成的海岸线和科赫曲线的性质极其相似，海岸线其实就是一种分形。

在生物身上也有分形的存在，科学家发现，我们人类的生命系统中，就有许多特征看起来像分形。

比方说，动脉和静脉血管的分布的形态，本质上就是分形。肾脏本身是有限的三维物体，而其中弯弯曲曲的血管就是按照分形的原理排布的。

你会发现，按照这么一个分形的原理来设计生命，是一个特别经济的选择。因为人类的DNA不需要记录下完整的设计图，血管一共要多长，这里要一段还是两段，那里是应该分叉还是应该走直线，要是记录完整的设计，信息量可太大了。而且具体到每个人，其实各不相同，如果是记录多套方案，然后给每个人随机挑选这么一套，那DNA承载的信息更是无法计数。

但是如果应用分形的原理，DNA并不需要存储那么多的信息，只需要记录若干简单的规则，然后不断重复使用这些规则，就能演化出复杂又各不相同的方案，经济又高效。

如果我们总结一下，你会发现，不论是「非线性系统」，还是「自我的复制」，都有相同的一个特点，就是系统中是有反馈的，也就是上一次的结束时的结果，影响了下一次的开始时的初始数值。

有了反馈，一个系统的变化率，就会受到之前变化结果的影响。变化率和变化结果互为因果，相互纠缠，这种复杂，就使得系统从秩序走向混沌，演化出了一个纷繁复杂的世界。

接下来，我们再来看第二个问题，混沌系统到哪里结束？

就像我们在前边讨论的，其实不会有无限放大的混沌系统，不然的话，巴西的一只蝴蝶引发了得州的龙卷风，得州的龙卷风引发了全美国的大海啸，全美的大海啸再引发世界级的寒潮，就这么层层放大，用不了多久银河系都毁灭了。

这当然和现实情况不相符。这就说明变化到了一定程度，混沌系统又会走向秩序。那从混沌到秩序的边界又在哪里呢？

科学家们对此做过各种各样的研究，他们的结论是，当混沌系统变得足够大，就会重新走向秩序。换句话说，大了就不一样。

比如我们前边举的例子，用水龙头创造一个混沌系统，当水龙头开到一定程度时，会随机出现各种各样的乱流，但是把水龙头开到最大，水流又变成单一整齐了。

甚至一些更奇特、更随机、更无法预测的事件，随着规模的增大，也会从混沌随机走向必然。

比如生命是怎么从地球上诞生的？很多人都说这是一个非常非常偶然的事件，但是，著名的圣塔菲研究所的一位科学家做了一个实验，发现生命的出现没有那么偶然。

我们知道，生命的出现最依赖的就是有机物，而有机物是地球上各种元素和物质经过复杂的化学反应之后产生的，是互动的结果。如果你听过郑路老师的社会网络课，就会知道，生命就是在各种物质组成的网络中诞生的。

圣塔菲研究所的这位科学家，就用纽扣模拟网络中的节点，用线模拟节点和节点的连接，他找了上万个纽扣，然后每一次都随机连接两个纽扣。

一开始的时候，这种连接是非常随机的，比如第一次，从一万个纽扣里边挑两个，大概会有将近5000万种不同的组合。可是科学家发现，随着连接的数量越来越多，规律就开始显现出来了。当连接的数量超过纽扣数量的一半时，就会形成超大规模的网络，把大多数纽扣连接起来。

你要知道，如果要保证1万个纽扣两两连接，你需要将近5000万条线，但是圣塔菲科学家的实验证明，只需要5000条线，就能把大部分纽扣吸纳进一个相互连通的物质网络当中了。

想象一下，在久远的地球上，物质A偶然和物质B发生了反应，产生了物质C，物质C又能和新的一种物质D发生反应。这种化学反应也像是在纽扣之间连线一样，当它们之间的连接变得越来越多，很快，就会把所有的物质都纳入这个网络中。所以，只要地球上一开始的物质是能生成有机物的，不缺材料，那么随着物质网络之间的互动，这些物质就一定能凑到一起去发生反应。

所以这本书中给出了一个惊人的结论：生命无可避免会出现，我们是大自然表达更深刻秩序的产物。

那到底为什么规模大了之后，系统就会从混沌重新走向秩序呢？说句实话，今天的科学家们还没法给出最终答案。在这本书中，作者给出了一个猜想，规模和秩序的关系，可能是因为熵增定律。到底什么是熵，时间有限，没法在这里向你展开介绍，得到上像万维钢老师的《精英日课》，孙亚飞老师的《化学通识30讲》当中，都有非常精彩的讲解，感兴趣的话你可以学习一下。

简单来说，如果没有外力干涉的情况下，所有系统都会向着熵增加的方向发展，这可能是宇宙的终极定律。规模越大，熵增加的方式就变得越少，用一个比喻来说，就有点像花钱，如果你想花出去100块钱，那有各种各样的方式，可是如果你想一下花出去100万，能选择的方式就少了很多，如果让你一下子花出去100个亿，那几乎就只有几种选择了。

系统也是如此，规模越大，能够使得熵增加的方式就变得越来越少，选择少了，确定性就增加了，规律和秩序就涌现出来了。

我们再来看第三个问题，研究混沌系统为什么这么重要？

许多科学家有一种共识，二十世纪人类科学史上三个最重要的理论，分别是相对论、量子力学和混沌理论。

这三个理论都是从某种程度上颠覆了传统的牛顿力学。相对论打破了牛顿力学最大的时空界限，也就是在以光年计算的大尺度宇宙空间里，或者在接近光速的情况下，牛顿力学就不再适用了，要用相对论才能解释。

量子力学呢，是打破了牛顿力学最小的时空界限，就是在原子、电子这些微小粒子的世界中，牛顿力学也不再适用了，要用量子力学才能解释。

而混沌理论呢，打破的是传统牛顿力学给科学家带来的一种信念，就是一切均可预测。

牛顿用它的三大力学定律，建立了一个简洁又精准的世界，从地上的苹果，到天上的星星，都能用一套规则来计算，并且每时每刻，都可以准确预测接下来的运动轨迹。

这就让科学家们产生了一种自信，就是只要我们能准确测定物体此时此刻的状态，接下来无穷无尽时刻的状态，我们就都能准则预言了。

但是现实给了科学家们一个巴掌，他们发现就是有那么一些问题，是没办法准确计算的。

比如著名的科幻小说《三体》，这本书的原型就是天文学上著名的「三体问题」，科学家发现，三颗恒星互相吸引，他们的运动轨迹，完全没有规律可循，根本没法计算和预测。

像是「三体问题」还有「蝴蝶效应」，这些现象让科学家们发现，就是有一些系统，内部变化是高度随机的，我们没法准确预测它每时每刻的状态。不是因为今天的计算能力不够，而是永远都不可能。

这让科学家们对于世界又有了新的认识，可以说，混沌理论，就是在画清楚混乱与秩序之间的边界。

当然，随着科学发展，不仅仅是有些我们以为拥有秩序的地方，现在被证明是混乱的。一些之前被认为混沌随机不可解释的现象，在混沌理论的帮助之下，开始变得清晰起来。

比如关于生命的问题。

到了20世纪中叶，所有简单的问题都有了答案。广义相对论与量子力学解释了宇宙在大尺度与小尺度中的运作机制，而人类对于DNA的结构以及它们在遗传复制机制中的了解，使得生命与演化在分子层次上能被简单地解释。

但生命是如何从无生命体中产生的？这个最有趣的问题，依然无解。宇宙中最难以用传统科学探索的、最复杂的生物，就是人类。

当简单的问题被解答了，很自然地，科学家会试图挑战复杂系统中更困难的问题。这个时候，混沌理论就开始发挥力量了。

前边咱们也提到了，像人体的形成，还有生命的诞生，其中复杂的过程，都能用混沌理论得到解释。甚至于，今天科学家们在探索外星生命时，也会用到混沌理论。

科学家发现，人类社会中有很多活动，都符合一个规律，就是事件的大小和发生概率的某个指数成反比。科学家把这个称之为「1/f噪声」，f就代表概率。

科学家们发现，我们人类说话，还有各种各样的音乐，不管是摇滚乐还是古典乐，都符合1/f噪声的特征。但是，随机的声音，比如收音机没有电台时候发出的声音，就不符合1/f噪声的特征。

甚至于，一些人类活动造成的影响，也会符合1/f噪声的特征。比如说，全球平均气温从19世纪中期开始上升，在升高的大趋势里边，也有起伏振荡，科学家研究发现，这些振荡就是1/f噪声。除此之外，像是城市堵车的情况，股市长期的起伏，这些曲线里边，都能看出1/f噪声来。

科学家们就提出了一种猜想，那就是这个1/f噪声里边，就隐藏着信息和秩序。通过扫描宇宙的信息，从中寻找1/f噪声，我们就能找到来自外星的文明与生命。

打个比方，这就像我们在大街上放一个录音机，录了一天之后回去听回放，我们能听见风声啊、喇叭声啊、鸟叫啊，这时突然听见了一串单词，就算是阿拉伯语或者西班牙语，咱们完全听不懂这些单词的意思，但是我们能听出抑扬顿挫和断句，所以我们能确定，刚才是有人在说话。

科学家在扫描宇宙的时候，也是如此，「1/f噪声」就像是这些单词，虽然我们可能看不明白这些信号到底代表着怎样的活动，但是我们可以确信，如果有这样的信号，那它的背后，一定不是随机的自然现象，而是有秩序的信息。

这个例子最能说明混沌系统这种「深奥的简洁」。宇宙中最复杂的事物，就是像我们一样的生命，生命的变化极其复杂难懂，但是通过混沌理论，我们却能找到生命的规律，找到简洁的方法，在茫茫宇宙中寻找我们的同类。

到这里，这本《深奥的简洁》其中精华的部分，我就为你解读完了。

总结一下，这本书讲的是，复杂的混沌系统背后，到底有什么样的规律？混沌系统是有边界的，就像是一个圈。这个圈里边就是混沌系统，变化无常难以预测，而圈子之外，就是秩序。

从秩序走向混沌，有两种最常见的方式，一种是「非线性系统」，另一种是「自我的复制」，这两种方式都有相同的一个特点，就是系统中是有反馈的，也就是上一次的结束时的结果，影响了下一次的开始时的初始数值。

有了反馈，一个系统的变化率，就会受到之前变化结果的影响。变化率和变化互为因果，相互纠缠，这种复杂，就使得系统从秩序走向混沌，演化出了一个纷繁复杂的世界。

而随着规模越来越大，系统又会从混沌回归到秩序，这种现象目前没有得到完全的解释，科学家的一个猜想是，规模越大，能够使得熵增加的方式就变得越来越少，选择少了，确定性就增加了，规律和秩序就涌现出来了。

今天，混沌理论在帮助我们探索宇宙和生命的秘密。人体的形成，还有生命的诞生，其中一些复杂的过程，都能通过混沌理论得到解释。甚至于，今天科学家们在探索外星生命时，也会用到混沌理论。

撰稿、讲述：陈章鱼 脑图：摩西脑图工作室

划重点

1. 从秩序走向混沌，有两种最常见的方式，一种是「非线性系统」，另一种是「自我的复制」。

2. 随着规模越来越大，系统又会从混沌回归到秩序。

3. 今天，混沌理论在帮助我们探索宇宙和生命的秘密。甚至于，今天科学家们在探索外星生命时，也会用到混沌理论。